Month: November 2018
Wavefront sensing
Introduction
Wavefront sensing is the act of sensing a wave front. As useless as this sentence gets, it is true and we perform this action with a wavefronts sensor… But if you bare with me, I promise that its going to be one of the coolest mix of science and technology that you will hear about! Actually, I promise that it would be even poetic, since that, in this post, you will learn why the stars twinkle in the sky!Just a little disclaim before I start: Im not an optical engineer and I understand very little about the subject. This post is just myself sharing my enthusiasm about this amazing subject.
Well, first of all, the word sensing just mean “measure”. Hence, wavefront sensing is the act of measure a wave front with a wavefront sensor. To understand what a wavefront measurement is, let me explain what a wavefront is and why one would want to measure it. It has to do with light. In a way, wavefront measurement is the closest we can get from measuring the “shape” of a light wave. The first time I came across this concept (here in the Geneva observatory) I asked myself: “What does that mean? Doesn’t light has the form of its source??”. I guess thats a fair question. In the technical use of the term measurement, we consider here that we want to measure the “shape” of the wave front that was originated in a point source of light very far away. You may say: “But thats just a plain wave!” and you would be right if we were in a complete homogeneous environment. If that were the case, we would have nothing to measure %-). So, what happens when we are in a non-homogenous medium? The answer is: The wavefront gets distorted, and we got to measure how distorted it is! When light propagates as a plain wave and it passes through an non-homogeneous medium, part of its wavefront slows down and others don’t. That creates a “shape” in the phase of the wavefront. Because of the difference in the index of refraction of the medium, in some locations, the oscillation of the electromagnetic arrives a bit earlier and some other it arrives a bit later. This creates a diferente in phase at each point in space. The following animation tries to convey this idea.

Figure 1: Wavefront distorted by a medium
As we see in the animation, the wavefront is plain before reaching the non-homogeneous medium (middle part). As it passes through the medium, it exits with a distorted wavefront. Since the wavefront is always traveling in a certain direction, we are only interested in measure it in a plane (in the case of the animation, a line) perpendicular to its direction of propagation.
In the animation above, a measurement at the left side would result in a constant value since, for all “y” values of the figure, the wave arrives at the same time. If we measure at the left side we get something like this
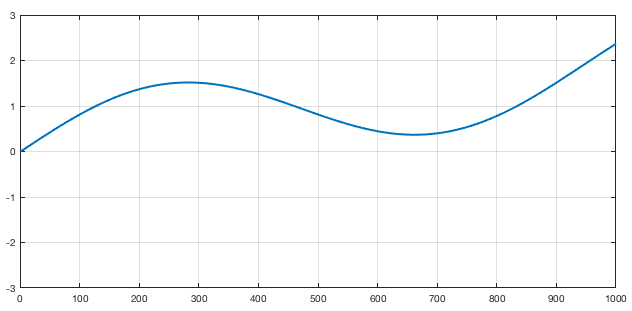
Figure 2: Wavefront measurement for the medium showed in Figure 1
Of course that, in a real wavefront, the measurement would be 2D (so the plot would be a surface plot).An obvious question at this point is: Why someone would want to measure a wavefront? There is a lot os applications in optics that requires the measurement of a wavefront. For instance, lens manufacturer would like to know if the shape of the lenses they manufactured is within a certain specification. So they shoot a plane wavefront through the lens of the glass and measure the deformation in the wavefront causes by the lens. By doing that, they measure the lens properties like astigmatism, coma and etc. Actually, did you ever asked yourself where those names (defocus, astigmatism, coma) came from? Nevertheless, one of the the most direct use of this wavefront measuring is in astronomy! Astronomers like to look at the stars. But the stars are very far away and, for us, they are an almost perfect point source of light. That means that we should receive a plain wave here right? Well if we did we have nothing to breath! Yes, the atmosphere is the worst enemy of the astronomers (thats why they spend millions and millions to put a telescope in orbit). When the light of the star or any object passes through the atmosphere, it gets distorted. Its wavefront make the objet’s image swirl and stretch randomly. Worst then that, the atmosphere is always changing its density due to things like wind, clouds and difference in temperatures. So, the wavefront follows this zigzags and THAT is why the stars twinkle in the sky! (I promise didn’t I? 😃) So, the astronomers build sophisticated mechanisms using adaptive optics to compensate for this twinkling and that involves, first of all, to measure the distortion of the wavefront.
Wavefront measurement
So, how the heck do we measure this wavefront? We could try to put small light sensors in an array and “sense” the electromagnetic waves that arrives at them… But light is pretty fast. It would be very very difficult to measure the time difference between the rival of the light in one sensor compared to the other (the animation in figure 1 is like a SUPER MEGA slow motion version of the reality). So, we have to be clever and appeal to the “jump of the cat” (expression we use in Brazil to mean a very smart move to solve a problem).
In fact, the solution is very clever! Although there are different kinds of wavefront sensors, the one I will explain here is called Shack–Hartmann wavefront sensor. The ideia is amazingly simple. Instead of measuring directly the phase of the wave (that would be difficult because light travels too fast) we could measure the “inclination” or the local direction of propagation of the wavefront. Now, instead of an array of light sensors that would try to measure the arrival time, we make an array of sensors that measure the local direction of the wavefront. With this information it is possible to recover the phase of the wavefront, but that is a technical detail. So, in summary, we only need to measure the angles of arrival of the wavefront. Figure 3 tries to exemplify that I mean:

Figure 3: Exemple of measurement of direction of arrival, instead of time of arrival.
Each horizontal division in the figure is a “sub-aperture” where we measure the inclination of the wavefront. Basically we measure the angle of arrival, instead of the time of arrival (or phase of arrival). If we do those sub-apertures small enough, we can reconstruct a good picture of the wavefront. Remember that for real wavefronts we have a plane, so we should measure TWO angles of arrival for each sub-aperture (the angle in x and the angle in y, considering that z is the direction of propagation).
At this point you might be thinking: “Wait… you just exchanged 6 for 12/2! How the heck do we measure this angle of arrival? It seems that this is far more difficult then to measure the phase itself!”. Now its time to get clever! The idea is to put a small camera in each sub aperture. Each tiny camera will be equipped with a tiny little lens to focus the portion of the wavefront to a certain pixel of this tiny camera! Doing that, at each camera, depending on the angle of arrival, the lens will focus the locally plain wave to a certain region of the camera dependent on the direction its traveling. That will make each camera see a small region with bright pixels. If we measure where those pixels are in relation to the center of the tiny camera, we have the angle of arrival!!! You might be thinking that its crazy to manufacture small cameras and small lenses in a reasonable packing. Actually, what happens is that we just have the tiny lenses in front of a big CCD. And it turns out that we don’t need hight resolution cameras in each sub-aperture. A typical wavefront sensor has 32×32 sub apertures, each one with a 16×16 grid os pixels. That is enough to give a very good estimation of the wavefront. Figure 4 shows a real image of a wavefront sensor.

Figure 4: Sample image from a real wavefront sensor
Simulations!
The principle is so simple that we can simulate it in several different ways. The first one is using the “light ray approach” for optics. This principle is the one we learn in college. Its the famous one that they put a stick figure on one side of a lens or a mirror and them draw some lines representing the light path. The wavefront sensor would be a bit more complex to draw, so we use the computer. Basically what I did was to make a simple blender file that contains a light source, something for the light to pass through (atmosphere) and the sensor itself. The sensor is just an 2D array of small lenses (each one made up by two spheres intersected) and a set of planes behind each lens to receive the light. We then set up a camera between the lenses and the planes to be able to render the array of planes, as they would be the CCD detectors of the wavefront sensor. Now we have to set the material for each object. The “detectors” must be something opaque so we could see the light focusing on it. The atmosphere have to be some kind of glass (with a relatively low index of refraction). The lenses also have glass as its material, but their index of refraction must be carefully adjusted so the focus of each one can be exactly on the detectors plane. Thats pretty much it (see figure 5).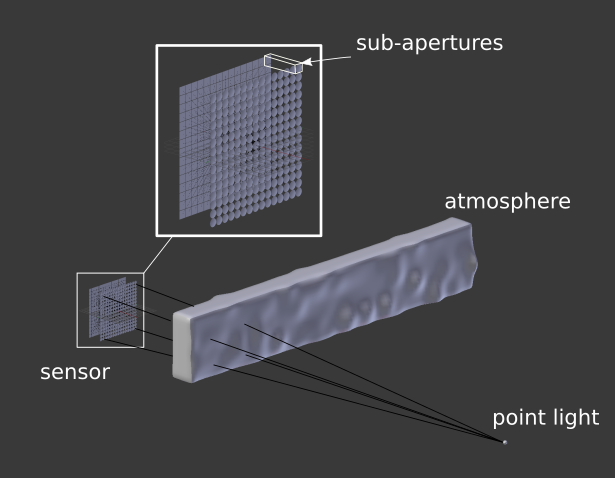
Figure 5: Setup for simulating a wavefront sensor in blender
To simulate the action, we move the “atmosphere” object back and forth and render each step. As light passes through the object, it diffracts it. That changes the direction of the light rays and simulates the wavefront being deformed. The result is showed in figure 6.
Figure 6: Render of the image on the wavefront sensor as we move the atmosphere simulating the real time reformation of the wavefront.
Another way of simulating the wavefront sensor is to simulate the light wave itself passing through different mediums, including the leses themselves and driving at some absorbing material (to emulate the detectors). That sounds kind of hardcore simulation stuff, and it kind of is. But, as I said in the “about” of this blog, I’m curious and hyperactive, so here we go: Maxwells equations simulation of a 1D wavefront sensor. To do that simulation, I used a code that I did a couple of yeas back. I’ll make a post about it some day. It is an implementation of a FD-TD (Finite Diferences in the Time Domain) method. This is a numerical method to solve partial differential equations. Basically, you set up your environment as a 2D grid with sources of electromagnetic field, material of each element on the grid and etc. Then, you run the interactive method to see the electromagnetic fields propagating. Anyway, I put some layers of conductive material to contain the wave is some points and to emulate the detector. Then I added a layer with small lenses with the right refraction index to emulate the sub-apartures. Finally, I put a monochromatic sinusoidal source in one place and pressed run. Voilá! You can see the result in the video bellow. The video contains the explanation of each element and, as you can see, the idea of a wavefront sensor is so brilliantly simple that we can simulate it at the Maxwells equation level!DIY (physical) experiment
To finish this post, let me show you that you can even build your own wavefront sensor “mockup” at home! What I did in this experiment was to build a physical version of the Shack–Hartmann principle. The idea is to use a “blank wall” as detector and a webcam to record the light that arrives at the wall. This way I can simulate a giant set of detectors. Now the difficult part: the sub-aperure lenses… For this one, I had to make the cat jump. Instead of an array of hundreds of lenses in front of the “detector wall”, I uses a toy laser that comes with those diffraction crystals that projects “little star-like patterns” (see figure 7).


|

|
Figure 7: 1 – Toy laser (black stick) held in place. 2 – green “blank wall”. 3 – Diffraction pattern that generates a regular set of little dots.
With this setup, it was time to do some coding. Basically I did some Matlab functions to capture the webcam image of the wall with the dots. On those functions I setup some calibration computations to compensate for the shape and place of the dots on the wall (see video bellow). That calibration will tell me where the “neutral” atmosphere will project the points (centers of the sub apertures). Them, for each frame, I capture and process the image from the webcam. For each image, I compute the position of the processed centers with respect to the calibrated ones. With this procedure, I have, for each dot, a vector that points form the center to where it is. That is exactly the wavefront direction that the toy laser is emulating!After that, it was a matter of having fun with the setup. I put all kinds of transparent materials in front of the laser and saw the “vector field” of the wavefront directions on screen. I even put my glasses and were able to see the same pattern the optical engineering saw when they were manufacturing the lenses! With a bit of effort I think I could even MEASURE (poorly of course) the level of astigmatism of my glasses!
The code is available in GitHub[2] but basically the loop consists in process each frame and show the vector field of the wavefront.
while 1
newIcap = cam.snapshot();
newI = newIcap(:,:,2);
newBW = segment(newI, th);
[newCx, newCy] = processImage(newBW, M, R);
z = sqrt((calibratedCy-newCy).^2 + (calibratedCx-newCx).^2);
zz = imresize(z,[480, 640]);
figure(1);
cla();
hold('on');
imagesc(zz(end:-1:1,:), 'alphadata',0.2)
quiver(calibratedCy, calibratedCx, calibratedCy-newCy, calibratedCx-newCx,'linewidth',2);
axis([1 640 1 480])
drawnow()
end
Conclusions
DIY projects are awesome for understanding theoretical concepts. In this case, the mix of simulation and practical implementation made very easy to understand how the device works. The use of the diffraction crystal in toy lasers is thought to be original, but I didn’t research a lot. If you know any experiment that uses this same principle, please let me know in the comments!Again, thank you for reading until here! Feel free to comment o share this post. If you are an optical engineer, please correct me at any mistake I might have made on this post. It does not intend to teach about optics, but rather to share my passion for this subject that I know so little!
Thank you for reading this post. I hope you liked it and, as always, feel free to comment, give me feedback, or share if you want! See you in the next post!
References
[1] – Shack–Hartmann wavefront sensor[2] – Matlab code
Uroflowmetry…
Introduction
This post is about health. Actually, its about a little project that implements a medical device called Uroflowmeter (not sure if that is the usual English word). Its a mouth full name to mean “little device that measures the flow of pee” (yes, pee as in urine 😇).Last year I had to perform an exam called Uroflowmetry (nothing serious, a lot people do that exam). The doctor said that, as the name implies, I had to measure “how fast I pee”. Technically it measures the flow of urine that flows when you urinate. At the time I thought to myself: “How the heck will he do that?”. Maybe be it was using a very sophisticated device, I didn’t know. Then he explained to me that I had to pee in a special toilet hooked up to a computer. He showed me the special device and left the room (it would be difficult if he stayed and watched hehehehehe). I didn’t see any sign of ultra technology anywhere. Then, I got the result and was nothing serious.
The exam result is a plot of flow vs time. Figure 1 shows an example of such exam. Since my case was a simple one, the only thing that matted in that exam was the maximum value. So, for me, the result was a single number (but I still had to do the whole exam and get the whole plot).
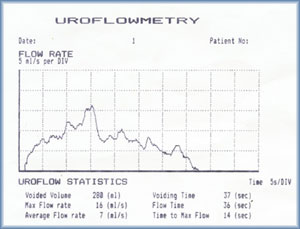 Figure 1 : Sample of a Uroflowmetry result[3]
Then, he prescribe a very common medicine to improve the results and told me that I would repeat the exam a couple of days later. After about 4 or 5 days I returned to the second exam. I repeated the whole process and peed on the USD $10,000.00 toilet. This time I did’t feel I did my “average” performance. I guess some times you are nervous, stressed or just not concentrated enough. So, as expected, the results were not ultra mega perfect. Long story short, the doctor acknowledge the result of the exam and conducted the rest of the visit (I’m fine, if you are wondering heheheh).
Figure 1 : Sample of a Uroflowmetry result[3]
Then, he prescribe a very common medicine to improve the results and told me that I would repeat the exam a couple of days later. After about 4 or 5 days I returned to the second exam. I repeated the whole process and peed on the USD $10,000.00 toilet. This time I did’t feel I did my “average” performance. I guess some times you are nervous, stressed or just not concentrated enough. So, as expected, the results were not ultra mega perfect. Long story short, the doctor acknowledge the result of the exam and conducted the rest of the visit (I’m fine, if you are wondering heheheh).
That exam got me thinking that it (the exam) did not capture the real “performance” of the act, by measuring only one flow. I might had notice some improvement with the medication, but I wasn’t so sure. So, how to be sure? Well, if only I could repeat the exam several times in several different situations… By doing that I could see the performance in average. I thought so seriously about that, that I asked the clinic how much does the exam costs. The lady in the desk said that it around $100,00 Brazil Reais ($30.00 USD, more or less in today’s rate). That was a bummer… The health insurance won’t simply pay lots of exams for me and if I were to make, say, 10 exams, it would cost me one thousand Brazil Reais. Besides, I would still have only 10 data points.
The project
Thinking about that, maybe I could measure it myself…? Then I decided to make my own “Urine flow meter”. it would be a Hardware / Software project, so I mediately though of using an Arduino (figure 2). The trick part is to measure the flow of something like urine. The solution I came up was to make an Arduino digital scale to measure the weight of the pee while I’m peeing on it (awkward or disgusting as it sounds %-). Then, I could measure the weight in real time at each, say, 20 to 50ms. Knowing the density of the fluid I’m testing I could compute the flow by differentiating the time measurement. Google told me that the density of urine is about 1.0025mg/l (if you are curious, its practically water actually). Later on I discovered that, that is exactly how some machine works, including the one I did the exams. Figure 2 : Arduino board
First I had to make the digital scale, so I used a load cell that had the right range for this project. The weight of the urine would range from 0 to 300~500mg more or less, so I acquire a 2Kg range load cell (Figure 3 and 4). I disassemble an old kitchen scale to use the “plate” that had the right space to hold the load cell and 3D printed a support in a heavy base to avoid errors in the measurements due to the flexing of the base. For that, I used a heavy ceramic tile that worked very well. The cell “driver” was an Arduino library called HX711. There is a cool youtube tutorial showing how to use this library [1].
Figure 2 : Arduino board
First I had to make the digital scale, so I used a load cell that had the right range for this project. The weight of the urine would range from 0 to 300~500mg more or less, so I acquire a 2Kg range load cell (Figure 3 and 4). I disassemble an old kitchen scale to use the “plate” that had the right space to hold the load cell and 3D printed a support in a heavy base to avoid errors in the measurements due to the flexing of the base. For that, I used a heavy ceramic tile that worked very well. The cell “driver” was an Arduino library called HX711. There is a cool youtube tutorial showing how to use this library [1].
 Figure 3 : Detail of the load cell used to make the digital scale.
Figure 3 : Detail of the load cell used to make the digital scale.
 Figure 4 : Loadcell connected to the driver HX711
The next problem was how to connect to the computer!!! This is not a regular project that you can assemble everything on your office and do tests. Remember that I had do pee on the hardware! I also didn’t want to bring a notebook to the bathroom every time I want to use it! the solution was to use a wifi module and communicate wirelessly. Figure 5 shows the module I used. Its an ESP8266. Now I could bring my prototype to the bathroom and pee on it while the data would be sent to the computer safely.
Figure 4 : Loadcell connected to the driver HX711
The next problem was how to connect to the computer!!! This is not a regular project that you can assemble everything on your office and do tests. Remember that I had do pee on the hardware! I also didn’t want to bring a notebook to the bathroom every time I want to use it! the solution was to use a wifi module and communicate wirelessly. Figure 5 shows the module I used. Its an ESP8266. Now I could bring my prototype to the bathroom and pee on it while the data would be sent to the computer safely.
 Figure 5 : ESP8266 connection to the Arduino board.
Figure 5 : ESP8266 connection to the Arduino board.



 Figure 6 : More pictures of the prototype
Once built, I had to calibrate it very precisely. I did some tests to measure the sensibility of the scale. I used an old lock and a small ball bearing to calibrate the scale. I went to the laboratory of Metrology at my university and a very nice technician in the lab (I’m so sorry I forgot his name, but he as very very kind) measures the weights of the lock and the ball bearing in a precision scale. Then I started to do some tests (see video bellow)
The last thing to make the prototype 100% finished was to have a funnel that had the right size. So I 3D printed a custom size funnel I could use (figure 7).
Figure 6 : More pictures of the prototype
Once built, I had to calibrate it very precisely. I did some tests to measure the sensibility of the scale. I used an old lock and a small ball bearing to calibrate the scale. I went to the laboratory of Metrology at my university and a very nice technician in the lab (I’m so sorry I forgot his name, but he as very very kind) measures the weights of the lock and the ball bearing in a precision scale. Then I started to do some tests (see video bellow)
The last thing to make the prototype 100% finished was to have a funnel that had the right size. So I 3D printed a custom size funnel I could use (figure 7).

 Figure 7: Final prototype ready to use
Once calibrated and ready to measure weights in real time, It was time to code the flow calculation. At first, this is a straight forward task, you just differentiate the measurements in time. Something like
$$
\begin{equation}
f[n] = \frac{{w[n – 1] – w[n]}}{{\rho \Delta t}}
\end{equation}
$$
Where \(f[n]\) and \(w[n]\) are the flow and weight at time \(n\). \(\rho\) is the density and \(\Delta t\) is the time between measurements.
Figure 7: Final prototype ready to use
Once calibrated and ready to measure weights in real time, It was time to code the flow calculation. At first, this is a straight forward task, you just differentiate the measurements in time. Something like
$$
\begin{equation}
f[n] = \frac{{w[n – 1] – w[n]}}{{\rho \Delta t}}
\end{equation}
$$
Where \(f[n]\) and \(w[n]\) are the flow and weight at time \(n\). \(\rho\) is the density and \(\Delta t\) is the time between measurements.
Unfortunately, that simple procedure is not enough to generate the plot I was hoping for. That’s because the data has too much noise. But I teach DSP, so I guess I could do some processing right 😇? Well I took the opportunity to test several algorithms (they are all in the source code at GitHub[2]). I won’t dive into details here about each one. The important thing is that the noise was largely because of the differentiation process so I tested filtering before and after compute the differentiation. The method that seemed to give better results was the spline method. Basically I got the flow data and averaged \(N\) fitted downsampled data with a spline. One sample of the results can be seen in figure 8.
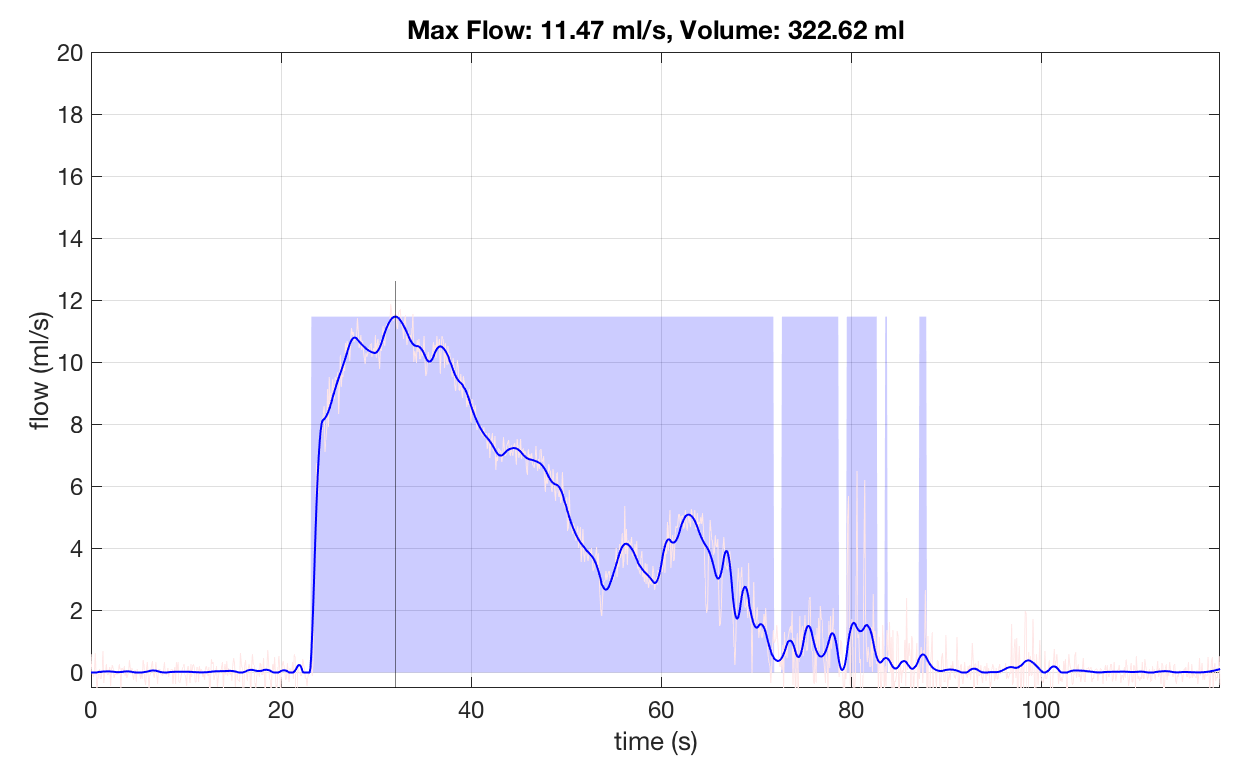 Figure 8 : Result of a typical exam done with the prototype.
The blue line is the filtered plot. The raw flow can be seen in light red. The black line tells where the max flow is and the blue regions estimates the non-zero flow (if you get several blue regions it means you stop peeing a lot in the same “go”). In the top of the plot you have the two numbers that the doctor is interested: The max flow and the total volume.
With everything working, it was time to use it! I spent 40 days using it and collected around 120 complete exams. Figure 9 shows all of them in one plot (just for the fun of it %-).
Figure 8 : Result of a typical exam done with the prototype.
The blue line is the filtered plot. The raw flow can be seen in light red. The black line tells where the max flow is and the blue regions estimates the non-zero flow (if you get several blue regions it means you stop peeing a lot in the same “go”). In the top of the plot you have the two numbers that the doctor is interested: The max flow and the total volume.
With everything working, it was time to use it! I spent 40 days using it and collected around 120 complete exams. Figure 9 shows all of them in one plot (just for the fun of it %-).
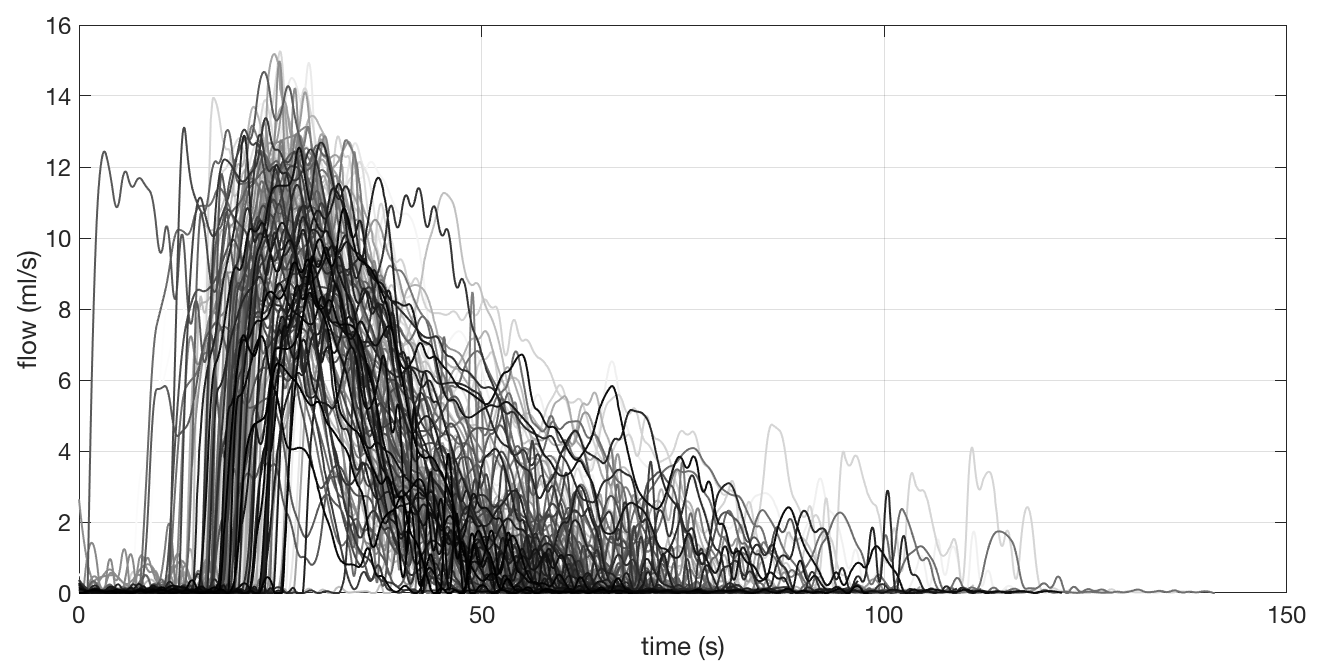 Figure 9 : 40 days of exams in one plot
Obviously, this plot is useless. To just show a lot of exams does not mean too much. Hence, what I did was to do the exams for some days without the medicine and then with the medicine. Then I separated only the max flow for each exam and plotted over time. Also, I computed the mean and the standard deviation for the points with and without the medicine and plotted in the same graph. The result is showed in figure 10.
Figure 9 : 40 days of exams in one plot
Obviously, this plot is useless. To just show a lot of exams does not mean too much. Hence, what I did was to do the exams for some days without the medicine and then with the medicine. Then I separated only the max flow for each exam and plotted over time. Also, I computed the mean and the standard deviation for the points with and without the medicine and plotted in the same graph. The result is showed in figure 10.
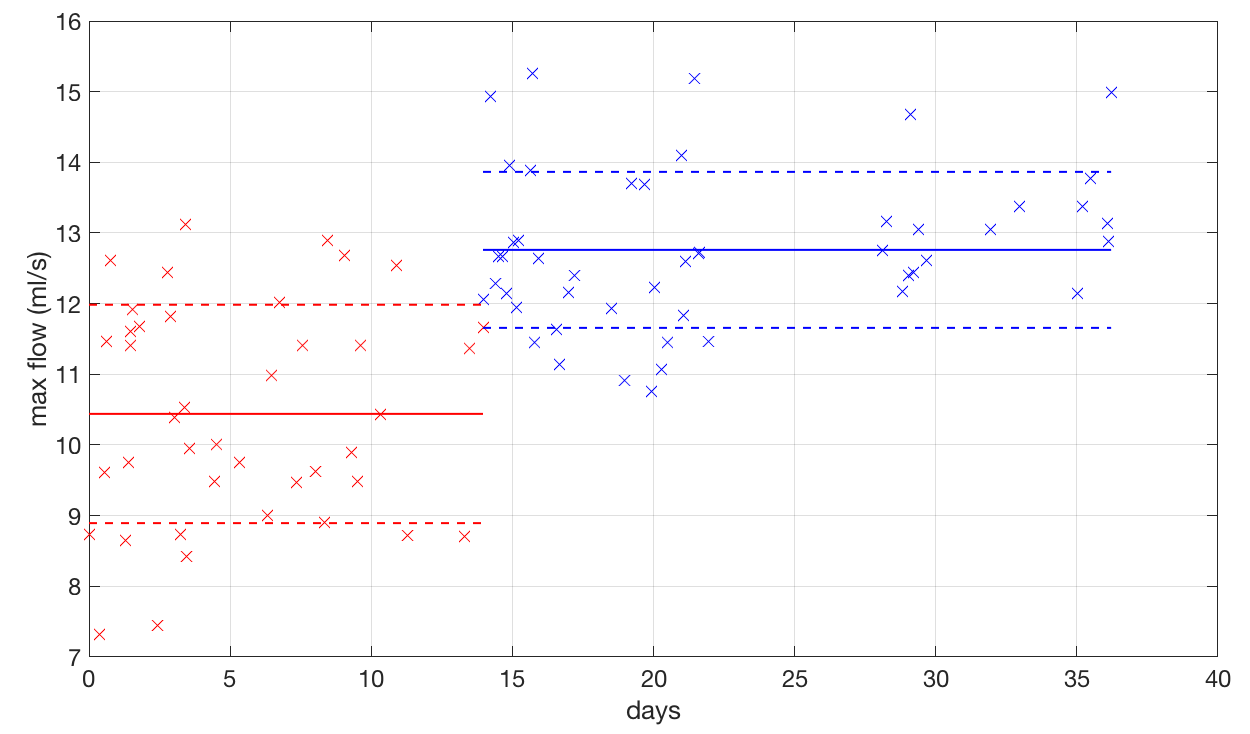 Figure 10 : Plot of max flow versus time. Red points are the results of max flow whiteout the medicine. The blue ones are the result with the medicine.
Well, as you can see, the medicine works a bit for me! The average for each situations is different and they are within more or less one standard deviation from each other. However, with this plot you can see that some times, even with the medicine, I got some low values… Those were the days I was not at my best for taking the water out of my knee. On the other hand, at some other days, even without the medicine, I was feeling like the bullet that killed Kennedy and got a good performance! In the end, statistically, I could prove that indeed the medicine was working.
Figure 10 : Plot of max flow versus time. Red points are the results of max flow whiteout the medicine. The blue ones are the result with the medicine.
Well, as you can see, the medicine works a bit for me! The average for each situations is different and they are within more or less one standard deviation from each other. However, with this plot you can see that some times, even with the medicine, I got some low values… Those were the days I was not at my best for taking the water out of my knee. On the other hand, at some other days, even without the medicine, I was feeling like the bullet that killed Kennedy and got a good performance! In the end, statistically, I could prove that indeed the medicine was working.
Conclusions
I was very happy that I could do this little project. Of course that this results can’t be used as a definite medical asset. I’m not a physician, so I’m not qualified to take any action whatsoever based on those results. I’ll show it to my doctor and he will decide what to do with them. The message I would like to transmit with it to my audience (students, friend, etc) is that, what you learn at the university is not just “stuff to pass on the exams”. They are things that you learn that can help a lot if you really understand them. This project didn’t need any special magical skill! Arduino is simple to use, the sensor and the wifi ESP have libraries. The formula to compute flow from weight is straight forward. Even the simple signal filtering that I used (moving average) got good results for the max flow value. Hence, I encourage you, technology enthusiast to try things out! Use the knowledge that you acquired in your undergrad studies! Its not only useful, its fun! Who would have thought that, at some point in my life, I would pee on one of my projects!!! 😅Thank you for reading this post. I hope you liked it and, as always, feel free to comment, give me feedback, or share if you like! See you in the next post!
References
[1] – Load cell[2] – Urofluximeter GitHub
[3] – NIDHI Uroflow
Simulating light
Intro
In this post I’ll try to describe one of my favorite “weekend projects”. Although it took almost a month to finish, I still call it a weekend project because I never used it for any senior research.Since I graduated in Electrical Engineering, I always wanted to simulate what I think is THE most fundamental system of equations for us (Electrical Engineers): The Maxwell’s equations. A couple of years back I finally had time to do so, and I’ll share with you the work I did. Everything is on GitHub, so if you want to try yourself, please feel free to fork the repository and play around!
In this post I’ll assume that you have at least a vague idea of what Maxwells equations are and that they describe how electromagnetic fields behave. Also, I assume that you know that light is a “moving electromagnetic field” (called electromagnetic wave). So, if we are able to describe and simulate electromagnetic waves, we can actually describe and simulate light!
Before show the simulations, let me start with a bit of explanation about the electromagnetic theory. The most obvious place to start is with Maxwell’s equations themselves: $$ \begin{equation} \begin{gathered} \nabla \cdot \vec E = \frac{\rho }{{{\varepsilon _0}}} \hfill \\ \nabla \cdot \vec B = 0 \hfill \\ \nabla \times \vec E = – \frac{{\partial \vec B}}{{\partial t}} \hfill \\ {c^2}\nabla \times \vec B = \frac{{\vec J}}{{{\varepsilon _0}}} + \frac{{\partial \vec E}}{{\partial t}} \hfill \\ \end{gathered} \end{equation} $$ These equations together with a couple of technical details like continuity constraints and boundary conditions, simply describes ALL physics related to electromagnetic fields. That includes radio waves, light, electricity, magnetism and etc. It is not the goal of this post to talk about Maxwell’s equation themselves, but rather about its solutions. In particular, about numeric solutions. Also, I do not intend to go deep into the theory of the simulation method, but rather to show its potential and encourage you to try! This post is not a tutorial, but I’ll try to point you in the right direction if you want to do it yourself. Also, I have to assume that you know some Calculus (at some not so basic level, I’m afraid).
First of all, lets understand what a solution to Maxwell’s equation means. Any equation that describes a physical phenomenon is a kind of mathematical description of that phenomenon. For instance, the famous Newton’s equation \(F = m\,a\) tells us that if you have a mass of \(10Kg\) and it is accelerating with an acceleration of \(2m/s^2\), there should be a force of \(20N\) being applied to the mass. In the same way, Maxwells equation tells us that if a medium has electrical permittivity \(\varepsilon_0\), the charge density is \(\rho\), etc, etc, then the electric and magnetic fields MUST be such that the divergent of the electric field is \(\rho / \varepsilon_0 \) and etc. For instance, Maxwell’s equation directly states that, whatever the situation is, the divergent of the magnetic field is zero. And so on…
So, that means that if you know the environment, in another words, you know how its permittivity, permissively, charge density, etc are distributed, you can predict how the electromagnetic fields will behave on this environment. In order to do that, you solve Maxwell’s equations to find \({\vec E}\) and \({\vec B}\).
It turns out that Maxwell’s equations, although they have a “simple” look, they are kind of “extensive” in the sense that the electric and magnetic fields have each one 3 components x, y and z and each component varies in space and time. Also they are partial differential equations, which involve all the derivatives of the solution either in x, y, z and t! So, to solve the Maxwell’s equation mean to find 6 functions of 4 variables. In general that is not possible to do analytically except in special cases. Hence, we have to appeal to numeric solutions. There are tons of methods for numerically solve a partial differential equation. In this post we will talk about the FD-TD method (due to Kane S. Yee) or method of Finite Diferences in the Time Domain (sometimes called Yee method). The method itself is pretty straightforward and, as all numerical method, it begins by exchanging the functions themselves by a grid of discrete values. As I mention, I won’t go deep into the method itself, but I’ll try to give an idea of how it works. Another important thing: I implemented the 2D version of the FD-TD method. So, the simulation will consist in a fields that is the same in the z direction form minus infinity to infinity. Unfortunately, cool things like polarization of light won’t be possible here (by definition, a 2D wave is aways polarized). But don’t worry, I promise that you can still have A LOT of fun with this apparently frustrating limitation.
In summary up to now, we will solve Maxwell’s equation numerically using the FD-TD method. So, what does this mean in practice? That means that we are going to divide our environment in a grid (2D for our case) and set each point on the grid with objects like conductors, sources, walls and etc. After that, we compute the electric and magnetic field on each point on the grid at each instant of time. The result is that, hopefully, we are going to see an “animation” of the fields interacting with our small “world”. Figure 1 tries to show a possible setup for a simple simulation.
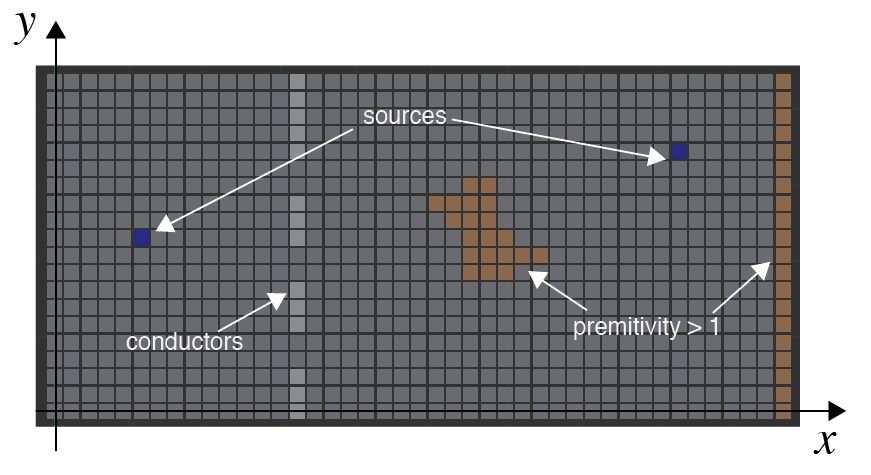
Figure 1: 2D grid with a source of electric field and some objects with different permittivities conductivities.
The FD-TD method itself[1] is well described in lots of places, books, etc. But if I were to recommend a place where you can learn very well, I would recumbent the youtube channel CEM lectures[2]. I saw some videos on FD-TD method and they are really good!Finite-Difference Time-Domain method
Here I’ll briefly describe the idea behind the method itself. The idea is based on the approximation of the derivatives by differences divided by the step. This principle is very well suited for ordinary differential equations that approximates derivatives in time. $$ \begin{array}{l} \frac{{dx(t)}}{{dt}} \approx \frac{{x(t + \Delta t) – x(t)}}{{\Delta t}}\\ x(t + \Delta t) \approx x(t) + \frac{{dx(t)}}{{dt}}\Delta t \end{array} $$ The time portion of the method is called “leapfrog” step and is based on this idea of integrating the time derivative. As you can see, it provides a way of computing the next value of the function \(x(t+\Delta t)\) used on its current values \(x(t)\). This is also called Euler’s method. In the FD-TD, method, the time derivative also depends on the derivative in space. Since we will focus on the 2D version, one of the fields (either the electric or the magnetic) will be the same in the z direction (z here is arbitrary). Depending on which you choose to be constant in the z direction, we call the setup as TE or TM (transverse electrical or transverse magnetic). All derivatives in z will be zero for the chosen field and it will not have x and y components. The other field then won’t have the z coordinate, only x and y. The reason this happens is that the curl of the field is a intrinsic 3D operation. In fact, although we simulate in a 2D world (even 1D for that matter) the fields are still three dimensional entities. What happens is that some components are zero or remans constant from minus infinity to infinity.
There is still one “trick” that must be done in the numerical setup for the FD-TD method. Since se have relationships with the curl of the fields, we have to consider the resulting vector to the in the “center” of the diferences. So, in the TM approach, the electric field have to be in the center of the magnetic fields (and no magnetic field must be present). So, for the method to work, we have to “stagger” the grid, moving it “half step” in x and y for one of the fields. So, this produces a grid for the electric field that is halfway displayed from the magnetic field. This is important for the assignment of the spacial indices for the electric and magnetic fields. Figure 2 shows the staggered grid that represents the electric and magnetic fields in the TM configuration.
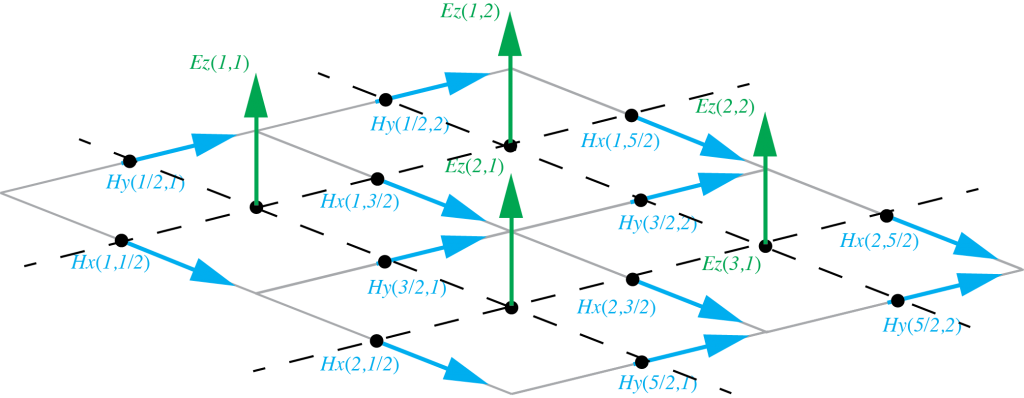
Figure 2: Staggered grid for the electric and magnetic fields in the TM scenario
As you can see, the staggered grid trick forces the electric field be always surrounded by magnetic field. This is perfect to approximate the curl equation. As a practical note, the “half” spatial step is just a notation stunt. In the end, in the computer, it will be all integer indices. This notation makes it easy to locate each field in the discrete approximation.Since we dealing with the 2D simulation, this simplifies the difference equations for the whole set of Maxwell’s equations. In fact we end up with this set of difference equations[3] bellow. Observe that the order of computation here matters… This is a technical detail that has to do with the stability of the method. Since we are integrating, if we do not compute things right, we might generate a systematic error in one of the fields, causing it to integrate more then necessary and blow up the values. $$ \begin{array}{l} {H_x}\left[ {m,n + \frac{1}{2},q + \frac{1}{2}} \right] = {H_x}\left[ {m,n + \frac{1}{2},q – \frac{1}{2}} \right] – \\ \frac{{\Delta t}}{{\mu \Delta y}}\left( {{E_z}\left[ {m,n + 1,q} \right] – {E_z}\left[ {m,n,q} \right]} \right) \end{array} $$ $$ \begin{array}{l} {H_y}\left[ {m + \frac{1}{2},n,q + \frac{1}{2}} \right] = {H_y}\left[ {m + \frac{1}{2},n,q – \frac{1}{2}} \right] + \\ \frac{{\Delta t}}{{\mu \Delta x}}\left( {{E_z}\left[ {m + 1,n,q} \right] – {E_z}\left[ {m,n,q} \right]} \right) \end{array} $$ $$ \begin{array}{l} {E_z}\left[ {m,n,q + 1} \right] = \frac{{2\varepsilon – \rho \Delta t}}{{2\varepsilon + \rho \Delta t}}{E_z}\left[ {m,n,q} \right] + \\ \frac{{2\varepsilon }}{{2\varepsilon + \rho \Delta t}}\left( \begin{array}{l} \frac{{\Delta t}}{{\varepsilon \Delta x}}\left( {{H_y}\left[ {m + \frac{1}{2},n,q + \frac{1}{2}} \right] – {H_y}\left[ {m – \frac{1}{2},n,q + \frac{1}{2}} \right]} \right)\\ – \frac{{\Delta t}}{{\varepsilon \Delta y}}\left( {{H_x}\left[ {m,n + \frac{1}{2},q + \frac{1}{2}} \right] – {H_x}\left[ {m,n – \frac{1}{2},q + \frac{1}{2}} \right]} \right) \end{array} \right) \end{array} $$ Now let me just comment a bit about the notation. \(E_z[m,n,q]\) is the electric field in z at index m and n in the grid at instant q in time (same for the other fields). \(\rho\), \(\epsilon\) and \(\mu\) are the conductivity, permittivity and permeability of the medium. Although not explicitly in the equations, each one also depend on the position on the grid m and n (\(\rho[m,n]\), \(\epsilon[m,n]\) and \(\mu[m,n]\)). The deltas are the spacing for the discretization in space and time.
Actually, the “algorithm” of FD-TD is pretty much only that! Its a loop that keeps updating the fields according to those equations. The heart of the implementation is the step that do that update. The code is as simple as this one
function [Ezo, Hxo, Hyo] = leapFrog2D(Ezi, Hxi, Hyi, parameters)
Ezo = Ezi;
Hxo = Hxi;
Hyo = Hyi;
c1 = parameters.c1;
c2 = parameters.c2;
c3 = parameters.c3;
c4 = parameters.c4;
dx = parameters.dx;
dy = parameters.dy;
boundary = parameters.boundary;
wire = parameters.wire;
Nx = size(Ezi,1);
Ny = size(Ezi,2);
j_p_0_E = 1:Nx-1;
j_p_0_E = 1:Ny-1;
i_p_1_E = 2:Nx;
j_p_1_E = 2:Ny;
i_p_0_H = 1:Nx-1;
j_p_0_H = 1:Ny-1;
i_p_1_H = 2:Nx;
j_p_1_H = 2:Ny;
% transverse electric
Ezo(i_p_1_E, j_p_1_E) = c1(i_p_1_E, j_p_1_E).*Ezi(i_p_1_E, j_p_1_E) + c2(i_p_1_E, j_p_1_E).*( ( wire(i_p_1_E, j_p_1_E).*Hyi(i_p_1_E, j_p_1_E) - wire(i_p_0_E, j_p_1_E).*Hyi(i_p_0_E, j_p_1_E) )/dx - ( wire(i_p_1_E, j_p_1_E).*Hxi(i_p_1_E, j_p_1_E) - wire(i_p_1_E, j_p_0_E).*Hxi(i_p_1_E, j_p_0_E) )/dy );
Hxo(i_p_0_H, j_p_0_H) = Hxi(i_p_0_H, j_p_0_H) + c3(i_p_0_H, j_p_0_H).*( ( wire(i_p_0_H, j_p_0_H).*Ezo(i_p_0_H, j_p_0_H) - wire(i_p_0_H, j_p_1_H).*Ezo(i_p_0_H, j_p_1_H) )/dy );
Hyo(i_p_0_H, j_p_0_H) = Hyi(i_p_0_H, j_p_0_H) + c4(i_p_0_H, j_p_0_H).*( ( wire(i_p_1_H, j_p_0_H).*Ezo(i_p_1_H, j_p_0_H) - wire(i_p_0_H, j_p_0_H).*Ezo(i_p_0_H, j_p_0_H) )/dx );
end
Having fun with it
With the implementation ready, it was time to have fun! I implemented a couple of auxiliary functions to “shape” the 2D world that will be simulated. They are functions to make basic shapes like squares, circles, lenses, and etc. With that, I created a lot of configurations that I will share here. For each one, I’ll put the vídeo of the simulation and comment on it. In all of the vídeos that you will see bellow, there is a basic setup. It consists of a source of electric field positioned, in general, on the left side of the grid. In the surrounding of the grid, there is what looks like a saw tooth border. That border is made of conducting material and aim to absorb the waves that reaches the border. If we do not use that object, the waves will perfectly reflect of the walls, creating a mess of waves inside the image. There is a more elegant solution to this problem called PML, or Perfect Matched Layer, but I didn’t implement that yet. The fields will be represented by a layer of red and blue colors. For visual convenience, I only plot the electric field intensity (red means positive values and blue, negative).A simple pulse of light
The first example is a kind of “hello world” of optics simulation. It consists only in the basic setup I mentioned where the source of electric field is just a “burst of light”. It is like a little lamp that lights on and off (very very quickly for the time scale of the simulation). The closest real situation that I can compare this simulation is a laser pulse. Its a short pulse that has a very well defined frequency.Single lens simulation
Here is where the fun begins. Now we have an example of a wave simulation of light passing through a lens and being focused on one “point”. The lens is just a region on the grid with a permittivity larger than one (its a lens for the electric field). The word “point” there is between quotation marks because, opposed to most of us learn in school optics, there no such thing as focal “point”. Because the wave nature of light, we can’t have a “delta function” as part of the solution of a set of first order partial differential equation (like Maxwell’s equations). Instead, we have a point where we reach a “limit” called diffraction limit of light. The size of this point depends on things like wavelength and focal distance. So, if some day you hear about a 1Giga Pixel camera inside a small smartphone, be caution! Someone is breaking the laws of nature and J. C. Maxwell is shaking like crazy on his thumb! 😂Another interesting thing that you can learn with this kind of simple example is that there is no such thing as “collimated” light! In another words, lasers are not perfect cylinders of light. They diverge! The difference is that the laser diverges as little as possible keeping the solutions for the wave propagation valid.
Actually, the subject of wave optics is a discipline in on itself. One cool thing that you can learn is that, at focal distance of the lens, instead of a “point” of light, we actually see the Fourier transform of whatever passes through the aperture as plane a wave!!!😱 For this example, since we have more or less a “plain” wave and the aperture is like a “square” (at least in 2D), what we see in the focal plane is the Fourier transform of the square pulse (a sinc function). If you look carefully at the focal distance of the lens, you can notice the first “side lobes” of the sinc forming along the y direction! This might become a new post entitles some thing like: “How to compute Fourier transforms with a piece of glass” %-).
Ha, I can’t forget to mention the “power density loss” that happens with electromagnetic waves. You can clearly see that, as the wave propagates from the source, the amplitude decays (the waves become fainter in the vídeo). Thats because the energy of the wave have to be distributed in a larger area. So, as the wave becomes “bigger” when it leaves the source, its amplitude have to decrease. Its like each “ring” of electric field has to have the same “volume”. So, small rings can be taller than the larger ones.
FSS
This one is a 2D version of a very interesting subject in electromagnetic theory that I learned with a very good professor and friend of mine, Antonio Luiz: Frequency Selective Surface. FSS’s are surfaces that “filters” the wave that hits them by reflecting part of the wave and transmitting the rest. They are amazingly simple to construct (no so much to tune) because they are basically a conductive surface formed by periodic shapes. In reality (3D world) they are an infinite plain made of little squares, circles, etc. The most common FSS in the world is the microwave door. It is just a metal screen made with small holes. That screen lets high frequencies pass (light) and reflect the low frequencies (the microwave that is dangerous and heat the food). So, thats why you see your food but at the same time you are protected from the microwaves.So, in a sense, this vídeo is nothing less than the simulation of a 2D microwave oven 😇! In the simulation you first see a pulse of high frequency content. It passes through the FSS (dashed line in the middle), reflecting some part. Then a second pulse of much higher wavelength is shot. This time, you barely see any wave transmitted, as this configuration is a high-pass FSS filter.
Antireflex coating and refraction
Now we will visit two subjects at once. The first is a simple one, but very cool to check with a simulation: Refraction of light. As we all learn in school optics, when light passes from one medium to another (with a different index of refraction), it refracts. “Refraction of light” is a phenomenon that have a couple of implications. When studying optics in school, we learn that light “bends” when reaches a different medium, changing the direction of propagation. We represent that with a little line that changes the angle inside the second medium. Just a side note: I think this representation of the light as a line is very very misleading for the students… If there is one thing that light is NOT, is a line. Its like representing time as a strawberry on physics 101… Anyway, the other thing that happens in the refraction of light is that its speed decreases in the medium with larger index of refraction. That is exactly what you see in this simulation. If you look carefully, the blue “glass” is 45 degrees tilted and the “light” comes out of the hole with the small lens horizontally. Due to refraction, the light “ray” inside the blue region is tilted down. Moreover, if you look even more carefully, you can see that inside the blue region, the distance between the red and blue part of the wave are smaller than it is outside. That mens that the wavelength is smaller inside the medium with larger index of refraction. The effect is that the light must travel slower to cope with the fact that, outside, the wave keeps coming with the same speed. Actually, in the simulation you can see that the propagation slows down inside the “glass”.The second concept present in this simulation is the concept of anti-reflex coating. This is a process that optical engineers have to do when fabricating lens, or even sheets of glass, to avoid reflection on the surface when light hits it. In the simulation, the upper “glass” has no treatment and the lower does. Because of that, you can clearly see that, when the wave hits the object whiteout the coating, there is a reflected wave going up, while in the surface with the coating, no wave is reflected.
Optical fiber
Every body must have heard about optical fibers… Then are small hair sized tubes made of glass (in general) that “conduct” light. They are based on another principle that we learn in school optics: Total internal reflection. This is like an “anti-refraction” effect. It happens when light hits an interface but the second medium has a index of refraction that is smaller then the one the light is propagating on. So the idea is that you shoot light into a tube and it will be confined inside because the outside medium (air or some other) has a index of refraction smaller then the one on the fiber. The light will them keep reflecting until reached a special end where it can be extracted.The video is practically self explanatory %-). We have two fibers. The cool thing about this is that, due to the 2D nature of the simulation, this fiber is not an actual “tube”. Rather, it is an infinite retangular region. But, so is our wave! Hence, the net effect is that we have the same behavior of internal reflection as an real optical fiber! Moreover, depending on the wavelength of our source, the propagation won’t be like a “reflecting” ray. Instead, if we have a larger wavelength source compared to the fiber diameter, the light will propagate like blobs of light. You can see that in the first fiber. There, the light seems to propagate in a straight path. That is the famous “mono-mode fiber”! The multimode fiber is the second one, where you have the reflection very well identifiable.
Crystal photonics wave guide
This one was fun to make. Not because of its structure, that is relatively simple, but because the “name of the simulation” sounded very sophisticated. The history of this one is more or less as follows; I was browsing the internet, probably reading the news, when I came across a paper[5][6] that talked about “Electro-optical modulation in two-dimensional photonic crystal linear waveguides”. I clicked in the pdf just out of curiosity and I came across an image that looked a lot like the waves I use to simulate. But the paper talked about a complex effect that light can present when you build a special microscopic structure for it. They use the same technique used to build microchips to build a lattice of silicon “crystals”. This lattice seems very simple in shape. They were just circles equally spaced with a “path” of missing circles. The paper said that, if you construct the circles with the right index of refraction and the right size (of the order of the wavelength of light that you want to use), you could “guide” the light in the path of missing crystals. Wow!! I though with myself: “Damn! That might be one of those super mega complex crazy math models that express a very special behavior of light in a ultra specific situation”. But then I remember that it had the word “linear” in the title of the paper. Well, I decide to loose 15min of my life to open photoshop and draw the same shape they used in the paper. Imported the image on the FD-TD simulator, followed more or less the rule for deciding the permittivity and wavelengths used and… Well, I couldn’t be happier! The video will speak for itself 😃! Simple as that! With no expertise whatsoever in the area of photonics, I was able to repeat the result of a paper that I spent 15min on…Wavefront sensor
One subject in optics that deserves its own post is the topic of “Wavefront sensing”. I’ll do this post for sure. For now, let me share only the FD-TD simulation of it, since we are in the topic of FD-TD. I can’t say much about this simulation other than it is simulating a device that really exists and is used to measure the “shape” of the light that arrives at it!!! I’ll let you curious (if you like this sorts of things %-) and I will talk about this simulation and the device itself in a separated post. Stay tuned!Optical circuit
Finally, just for the heck of it, let me show a simulation with a larger setup. This is just to show that, with the simulator implemented, to simulate a complex environment is just a matter of setting it up. So, In this one, the bended fiber optics and the waveguide are images that I made in photoshop and imported as permittivities in the simulator! So, this is it… Is THAT easy to simulate a complex environment. Draw it in paint if you like, and use as parameters for the simulator %-). The vídeo is also self explanatory at this point. We have the source of light as usual, an optical fiber and a waveguide that guides the light pulses!Going a bit further with the fun
Finally (this is the last one, I promise) let me share the tipping point of my excitement (up to now) with FD-TD. All the vídeos you saw up to now are “standard” in the sense that everyone that works with FD-TD do small animations like those. Even the colors are kind of a tabu (red and blue). So, I wanted to do something different. But what could be different in this kind of animations? Them I turned to a software that I love with all my heart: Blender. Its a 3D software (like AutoCAD, but way cooler %-). One of the coolest things of Blender is that you can implement scripts in python for it. So, what if I, some how, were able to communicate Matlab with Blender and “render” the animations on its cool 3D environment? And thats what I did… I set up a simple 3D scene and plotted the electric field as a Blender object and, at each frame, rendered the screen. I even put a fake voltmeter to fakely measure the “source amplitude” heheheheh. I think it is very cute to see the little waves propagating on the surface of the object.Even further…
Since I had the 3D file for the frames, why not to 3D print one them? That, I would guess, is original… I have a feeling that I was the first crazy person in the planet to 3D print the solution of Maxwell’s equation on yellow PLA… See figure bellow %-) Figure 3: The ways you can visualize the solution to Maxwell’s equation for a boundary condition involving a source, a lens and a tilted glass block.
Figure 3: The ways you can visualize the solution to Maxwell’s equation for a boundary condition involving a source, a lens and a tilted glass block.
Conclusions
It is amazing how much knowledge can be extracted from such simple implementation (a loop that calls a function with a simple update rule). The heart of the FD-TD algorithm does not involve while loops or if statements. There is no complex data structures, no weird algorithms and crazy advanced math calculation in the code. Just something like \(E[n+1] = E[n] + …\)… In the end, the algorithm itself, uses only the 4 mathematical operations. This is the power of Maxwell’s equation. Obviously, we put some considerable effort in the “boundary conditions” by organizing the permittivities, conductivities, etc. But that is a “drawing” effort. The big magic happens because we have such special and carefully crafted relations in the Maxwell’s equations. Nature is REALY amazing!As I said in the beginning of this post, this is one of my favorite “weekend project”. Not only because I always wanted to simulate Maxwell’s equations themselves. Actually, after I started to play with it, I learned a lot of what is considered very complicated concepts without even notice that I was learning it! One situation that I will aways remember is that, after I arrive in my second post-doc in the Genevra Observatory, I was very scary that I would not understand the optics part of the project. But for my surprise, as I started hearing terms like “diffraction limit”, “point spread function”, “anti-reflex coating”, “sub-aperture” and etc, I began to associate those terms to stuff that I actually saw in my situations, hence knowing exactly what they were!!! That is a feeling that I, as a professor, can’t have enough of.
Thank you for reading this post. I hope you liked reading it as much as I liked writing it! As aways, feel free to comment or share this post as much as you want!
References
[1] – Finite-Diference Time-Domain method[2] – CEM Lectures
[3] – John B. Schneider, Understanding the Finite-Difference Time-Domain Method
[4] – FD-TF GitHub
[5] – Electro-optical modulation in two-dimensional photonic crystal linear waveguides
[6] – Waveguide Bends in Photonic Crystals
WhatsApp memes with hidden beauty!
Intro
I love internet memes. They provide a funny way to convey a message or an idea. As a professor, I cherish all didactic mechanisms and anything that easy the acquisition or fixation of ideias and concepts. In fact, I find memes to be a very useful didactic tool. I might make a post only about didactic memes in the future. Right now I want to talk about one specific meme that, although not didactic at first glance, hides a cool and rather formal math concept without most people realizing it (except for the author, I bet!).The fun…
So, here we go. This is the meme. Maybe you already received it via WhatsApp (I did %-).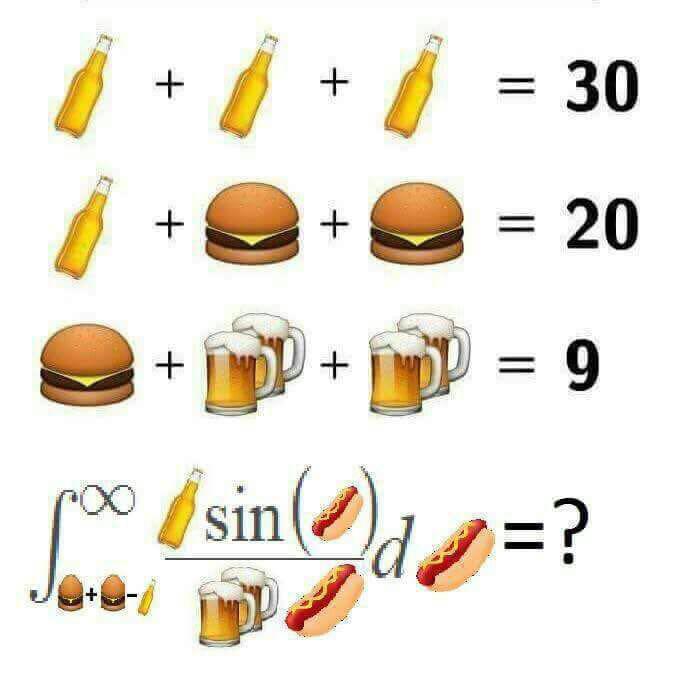 The beginning of the meme is, as you most probably know, those famous “linear system of equations with emojis as variable names”. Fun fact about those memes: Most of them present systems that are quasi triangular, and hence, very very easy to solve. Anyways… In general, they give you 3 or 4 equations with right hand side values and asks you to compute a 4th or 5th equation that is, in general, another linear combination of the variables.
The beginning of the meme is, as you most probably know, those famous “linear system of equations with emojis as variable names”. Fun fact about those memes: Most of them present systems that are quasi triangular, and hence, very very easy to solve. Anyways… In general, they give you 3 or 4 equations with right hand side values and asks you to compute a 4th or 5th equation that is, in general, another linear combination of the variables.
In the case of the meme in this post, the 4th equation is nothing like a linear combination of the values. In fact, it is some weird looking complex mathematical aberration! This is where the meme ends for most people. The funny in that meme is that nobody can solve it. So, you suppose to send that to your annoying friend that keeps sending regular linear combination meme to you, solving all of them to show that he is a math genius.
Well… It turns out that the 4th equation is solvable! Moreover, it involves the integral of a very famous function (\(sinc(x)\)) which has a very elegant solution for when the limits involves infinity and zero. And yet more, that is despite the fact that it have no closed form solution for arbitrary limits.
Translating the emojis to variables, we arrive at the following integral $$\int\limits_{2b – a}^\infty {\frac{{a\sin (x)}}{{c\,x}}{\text{d}}x}$$ which, with numbers (solving the trivial linear system of emojis), becomes $$ 5\int\limits_0^\infty {\frac{{\sin (x)}}{x}{\text{d}}x} $$ The goal of this post them, is to solve this integral using almost all steps as purely algebraic manipulations. We are also going to use rules of calculus too, obviously. Moreover, we will have to go though some complex numbers too (yes, we go that deep in a innocent internet meme). Lets now solve the sinc function integral.
We start by acknowledging that \(sin(x)/x\) is a function with an anti-derivative that is very hard to find. If only we had something to relate easier functions to integrate (like exponentials)… But wait, we have! The first exponential that we can exchange, is the sine function (as you probably already guessed). So lets use Euler’s identity: $$ \sin (s) = \frac{{{e^{sj}} – {e^{ – sj}}}}{{2j}} $$ Although this is not a pure algebraic step, I will save the Taylor expansion prove of this one, for it is a very, very known relation.
The second one is the “jump of the cat” as we say in my country. I found that in an awesome StackExchange answer[1]. It has to do with the Laplace transform of the step function $u(t)$. In short, it states that the Laplace of the step function is the inverse function. The relation has a simple one line of proof as $$ L\left\{ {u(t)} \right\} = \int\limits_0^\infty {{e^{ – st}}{\text{d}}t} = \left. {\frac{{{e^{ – st}} – {e^{ – st}}}}{{ – s}}} \right|_0^\infty = \frac{1}{s} $$ Hence $$ \int\limits_0^\infty {{e^{ – st}}{\text{d}}t} = \frac{1}{s} $$ Holly butter ball! Now we can relate the inverse function with the exponential 😱. I wish I could use emojis on technical papers. They convey so much of the authors wonder when some beautiful math trick is used… %-)
Now lets change the names of the variables to $$ \int\limits_0^\infty {\frac{{\sin (s)}}{s}{\text{d}}s} $$ which makes our original sinc integral to become $$ \int\limits_0^\infty {\int\limits_0^\infty {{e^{ – st}}\frac{{{e^{sj}} – {e^{ – sj}}}}{{2j}}{\text{d}}t} {\text{d}}s} $$ Ok, the \(s\) integral is easy and here are the steps to solve it (it’s an exponential integral) $$ \begin{gathered} \frac{1}{{2j}}\int\limits_0^\infty {\int\limits_0^\infty {{e^{ – s(t – j)}} – {e^{ – s(t + j)}}{\text{d}}s} {\text{d}}t} \\ \frac{1}{{2j}}\int\limits_0^\infty {\left. { – \frac{{{e^{ – s(t – j)}}}}{{t – j}} + \frac{{{e^{ – s(t + j)}}}}{{t + j}}} \right|_0^\infty {\text{d}}t} \\ \frac{1}{{2j}}\int\limits_0^\infty { – \frac{{{e^{ – \infty (t – j)}}}}{{t – j}} – \frac{{{e^{ – \infty (t + j)}}}}{{t + j}} + \frac{{{e^{ – 0(t – j)}}}}{{t – j}} – \frac{{{e^{ – 0(t + j)}}}}{{t + j}}{\text{d}}t} \\ \frac{1}{{2j}}\int\limits_0^\infty {\frac{1}{{t – j}} – \frac{1}{{t + j}}{\text{d}}t} \end{gathered} $$ Now we have a integral in \(t\). This one is a lot of fun. Lets start by separating the two integrals as $$ \begin{gathered} \frac{1}{{2j}}\int\limits_0^\infty {\frac{1}{{t – j}}{\text{d}}t} – \frac{1}{{2j}}\int\limits_0^\infty {\frac{1}{{t + j}}{\text{d}}t} \end{gathered} $$ and do the following substitution. $$ \begin{gathered} {u_1} = t – j \\ d{u_1} = dt \\ {u_2} = t + j \\ d{u_2} = dt \\ \end{gathered} $$ Now we foresee that we are going to have some trouble with this infinity and the logs that will appear… Hum… Lets be careful (to not say formal) and wrap that around a limit. We deal with the limit later. Ok, so we have the following inverse integral (with is also simple to solve inside the limit) $$ \begin{gathered} \frac{1}{{2j}}\mathop {\lim }\limits_{a \to \infty } \int\limits_{ – j}^{a – j} {\frac{1}{{{u_1}}}{\text{d}}{u_1}} – \int\limits_j^{a + j} {\frac{1}{{{u_2}}}{\text{d}}{u_2}} \\ \frac{1}{{2j}}\mathop {\lim }\limits_{a \to \infty } \left. {\ln ({u_1})} \right|_{ – j}^{a – j} – \left. {\ln ({u_1})} \right|_j^{a + j} \\ \frac{1}{{2j}}\mathop {\lim }\limits_{a \to \infty } \ln (a – j) – \ln ( – j) – \ln (a + j) + \ln (j) \\ \frac{1}{{2j}}\mathop {\lim }\limits_{a \to \infty } \ln (a – j) – \ln (a + j) + \ln (j) – \ln ( – j) \\ \frac{1}{{2j}}\mathop {\lim }\limits_{a \to \infty } \ln (a – j) – \ln (a + j) + \ln \left( {\frac{j}{{ – j}}} \right) \\ \frac{{\ln \left( { – 1} \right)}}{{2j}} + \frac{1}{{2j}}\mathop {\lim }\limits_{a \to \infty } \ln (a – j) – \ln (a + j) \end{gathered} $$ The lets now investigate this peculiar limit (and begin the fun part). We start by acknowledging that it is a complex-number limit, hence not straight forward to evaluate. Then, we do the second “jump of the cat” (small when compared with the Laplace one before) and change the limit of infinity with a limit to zero as $$ \begin{gathered} \mathop {\lim }\limits_{a \to \infty } \ln (a – j) – \ln (a + j) \hfill \\ \mathop {\lim }\limits_{a \to 0} \ln \left( {\frac{1}{a} – j} \right) – \ln \left( {\frac{1}{a} + j} \right) \end{gathered} $$ Now we just do some algebraic steps as follows $$ \begin{gathered} \mathop {\lim }\limits_{a \to 0} \ln \left( {\frac{{1 – aj}}{a}} \right) – \ln \left( {\frac{{1 + aj}}{a}} \right) \hfill \\ \mathop {\lim }\limits_{a \to 0} \ln \left( {1 – aj} \right) – \ln (a) – \ln \left( {1 + aj} \right) + \ln (a) \hfill \\ \mathop {\lim }\limits_{a \to 0} \ln \left( {1 – aj} \right) – \ln \left( {1 + aj} \right) \end{gathered} $$ And voilá! Put \(a=0\) and we have out first part of the integral $$ \ln \left( 1 \right) – \ln \left( 1 \right) = 0 $$ Now we have to figure what the heck is this negative logarithm thing… $$ \begin{equation} \frac{{\ln \left( { – 1} \right)}}{{2j}} \end{equation} $$ To do that, lets make the cat jump again and write -1 as \(e^{j\,\pi}\)
now we have $$ \begin{equation} \frac{{\ln \left( { – 1} \right)}}{{2j}} = \frac{{\ln \left( {{e^{j\pi }}} \right)}}{{2j}} \end{equation} $$ which is just \(\frac{\pi }{2} \). %-)
Finally coming back to the original integral we have $$ 5\int\limits_0^\infty {\frac{{\sin (x)}}{x}{\text{d}}x} = \frac{5\,\pi}{2}$$ Which is the actual answer for the meme %-).
Conclusion
So, if you see this meme on your WhatsApp, feel free to answer in a very “disdain” way: “Humpf! This is trivially equal to \(\frac{5\,\pi }{2} \)!”. If they doubt you, share this post with them %-).I hope you like this post! Feel free to share it or use any of this derivations on your own proofs! See you in the next post!